带括号的四则混合运算计算器（三）

在表达式中加入变量有什么用呢？看看下图就知道了：

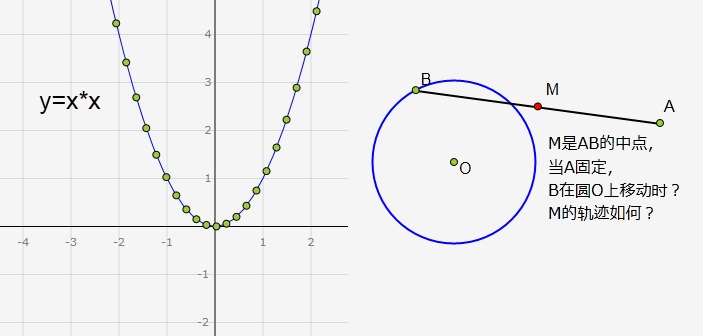
含有x的表达式无法直接求值，需要先对x进行赋值，例如对于(y=x*x)不断的赋值、取值，可以绘制出一一列点(x,y),从而可以绘制出平滑的抛物线。

所以，XNode节点必须有个可赋值的属性:XValue,而且应该是静态的，以下是XNode的定义：

public class XNode : NodeBase
{
    public static double XValue { get; set; }
    public XNode(int index, string data, string expression)
    : base(index, data, expression)
    {
    }
    public override double GetValue()
    {
        return XValue;
    }
}

变量、常量的节点只要一次性解析完毕，以后的表达式重构中就不会再出现了，因此可以继承IExpressionAdjustor进行事先处理，处理完成后可以将XFinder从finders中移除以提高性能。

以下是XFinder的定义：

public class XFinder : FinderBase,IExpressionAdjustor
{
    public override int Priority { get { return (int)FinderPriority.XFinder; } }
    protected override string Rule
    {
        get { return @"x"; }
    }
    protected override INode GenerateNode(string sourceExpression, string data, int index)
    {
        if (sourceExpression.Length > Match.Index + Match.Value.Length)
        {
            var tailChar = sourceExpression[Match.Index + Match.Value.Length];
            //如果后面一个字符是':'或者是[a-zA-Z],则它是一个函数中的字符，不当做变量处理，否则当做变量
            if (tailChar == '(' || (tailChar >= 'a' && tailChar <= 'z') || (tailChar >= 'A' && tailChar <= 'Z'))
            return null;
        }
        return new XNode(index, data, sourceExpression);
    }
    //重构原始表达式，并生成每个函数的Finder实例
    public void AdjustExpression(ref string expression, ref List<IFinder> finders)
    {
        while (true)
        {
            INode node = Find(expression);
            if (node == null) break;
            AddNode(Calculator.FoundNodes, node);
            expression = expression.ReplaceOnce(node.Value, node.Id, node.Index);
        }
        finders = finders.Except(new List<IFinder> { this }).ToList(); //当前类的职责已经结束，将其移除
    }
}

由于含变量的表达式无法直接求值，Calculator中CalculateExpression方法也就不够用了，我们需要提供另外一个方法：GetValue(double x)以实现对变量的先赋值再取值。

以下是更新后的Calculator类，可以看出为了使用方便我们还提供了一个GetValues()的方法：

public class Calculator
{
    private List<INode> _foundNodes;
    public List<INode> FoundNodes { get { return _foundNodes; } }
    public INode RootNode { get { return FoundNodes.Last(); } }
    public double CalculateExpression(string expression)
    {
        _foundNodes = new List<INode>();
        FinderBase.FindAllNodes(this, ref expression);
        if (FoundNodes != null && FoundNodes.Count >= 1)
        return RootNode.GetValue();
        return double.NaN;
    }
    public double GetValue(double x)
    {
        XNode.XValue = x;
        return RootNode.GetValue();
    }
    //例如可以返回Points：(x1,y1),(x2,y2)...
    public List<Tuple<double, double>> GetValues(double xFrom, double xTo, int steps)
    {
        double oneStep = (xTo - xFrom)/steps;
        var rlt = new List<Tuple<double, double>>();
        for (int i = 0; i < steps; i++)
        {
            XNode.XValue = xFrom + oneStep*i;
            RootNode.GetValue();
            rlt.Add(new Tuple<double, double>(XNode.XValue, RootNode.GetValue()));
        }
        return rlt;
    }
    internal INode GetNode(string id)
    {
        return FoundNodes.FirstOrDefault(n => n.Id == id);
    }
}

注意，第一次调用GetValue()方法之前必须先调用CalculateExpression()进行节点解析，此后就不需要进行解析了，因为直接使用解析出来的Nodes就可以了。

怎么展示X的美妙之处呢？对，画图演示，下面来说说平面直角坐标系：

有关数学上的平面直角坐标系与电脑的屏幕坐标系，如果有不熟悉的请参考数学编程的独立课程。归纳一下是以下三点：

Y轴方向相反。
原点位置（屏幕或者说UI控件如（Canvas）的坐标系原点在左上角顶点，数学坐标系通常在中心）
单位（屏幕坐标系通常以像素为单位，数学坐标系通常以单元(例如以1厘米为一个单元)）

好了，有了这些差别，势必涉及到数学转换，例如屏幕上的位置（PhysicalPoint）转换为数学逻辑上的位置（LogicalPoint）。.net已经有了Point类型表示一个位置，我们可以直接用它，不过在这里为了避免混淆，我们还是先分别定义PhysicalPoint和LogicalPoint两个类：

public class LogicalPoint:PointBase
{
    public LogicalPoint (double x,double y) : base(x,y){}
    public override PhysicalPoint ToPhysical(CoordinateSystem cs)
    {
        return  cs.ToPhysical(this);
    }
}
public class PhysicalPoint : PointBase
{
    public PhysicalPoint(double x, double y) : base(x,y){}
    public override LogicalPoint ToLogical(CoordinateSystem cs)
    {
        return cs.ToLogical(this);
    }
}

转换必然会用到CoordinateSystem，就是我们定义的数学坐标系，因为我们可能会用到多个坐标系，而每个的单位长度可能不一样，以下是的CoordinateSystem定义，我们直接继承Canvas，因为坐标系通常要画坐标轴和刻度，当然也可以采用聚合的方法，将Canvas作为CoordinateSystem的一个属性来实现。

public class CoordinateSystem:Canvas
{
    public CoordinateSystem(double width,double height)
    {
        this.Width = width;
        this.Height = height;
        Origin = new PhysicalPoint(width/2, height/2);
    }
    private PhysicalPoint Origin;
    private const double UnitLength = 50;//每单位长度对应的屏幕像素
    #region Coordinate transforms
    public LogicalPoint ToLogical(PhysicalPoint p)
    {
        return new LogicalPoint((p.X - Origin.X) / UnitLength, -(p.Y - Origin.Y) / UnitLength);
    }
    public PhysicalPoint ToPhysical(LogicalPoint p)
    {
        return new PhysicalPoint(Origin.X + p.X * UnitLength, Origin.Y - p.Y * UnitLength);
    }
    #endregion
}

好了，下面是运行截图，是不是比以前酷多了！

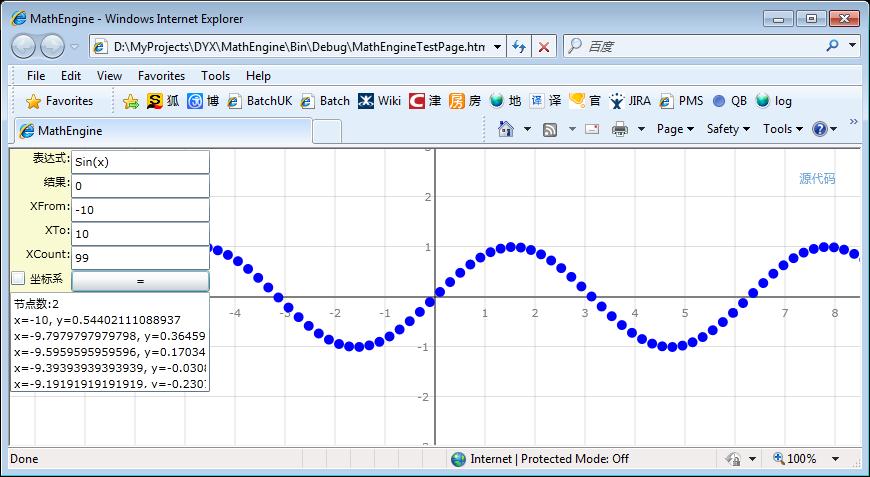
但是为什么只有点，任然没有见到传说中的曲线呢？实现曲线还是有难度！如果我们直接将点与点用线段连起来，那对于像Sin(x)这样的表达式没问题，如果对于Sin(1/x)呢？

下一部分我们将对之前的所作所为做个总结，具体是加入动画演示来更形象的表述表达式解析和求值的过程，从而达到更加形象教学的目的！

数学编程

第二部分：编程技能的简单应用

带括号的四则混合运算计算器（三）