带括号的四则混合运算计算器（一）

这一节，我们教大家学会开发我们学习过程中经常要用的工具：电子计算器。

本文用到的相关技术细节主要有以下几点，如果不熟悉可以先参考一下相关的技术资料：

TDD(测试驱动开发)：本文只是将其作为一个完整的项目开发的一部分简单提及。
设计模式：真正的面向对象设计必然遵循了一种或几种模式，本文会适当地方加以注释。
正则表达式：仅用到非常简单的正则式用于表达式解析，如果对正则表达式不了解，花20分钟速成一下即可掌握：）

下面就开始我们的系统开发！

（一）项目建立：用VisualStudio建立两个项目，主项目MathEngine和测试项目MathEngineTests。

（二）编写测试用例：首先，TDD是要先从业务的角度编写系统测试用例，在此之前我们不需要考虑程序设计方面的东西。严格来说TDD是需要两个人相互合作交互编码和测试，这个过程贯穿于开发的整个过程。下图是我们项目开始的测试用例：

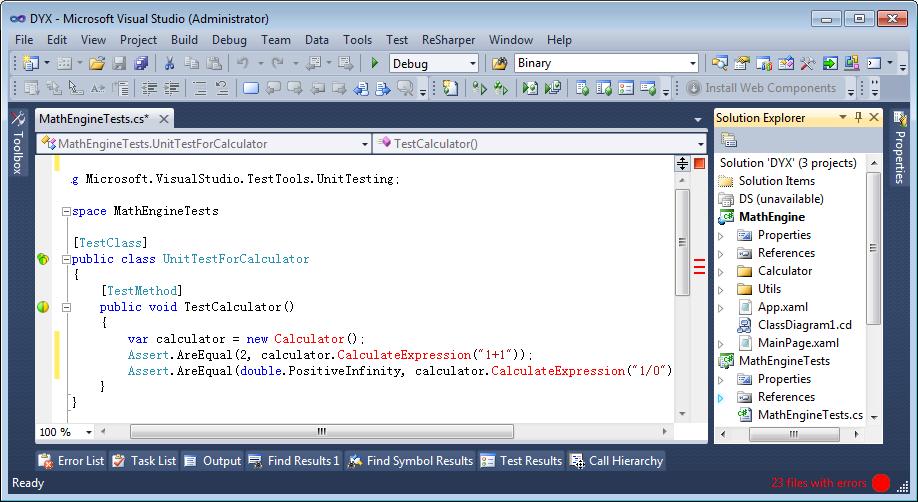
可以看出来，编写测试用例时，还没有进行编码，因此编写测试用例同时也是一个对类和类的接口进行概要设计的过程。

Calculator和其方法CalculatorExpression都不存在，我们可以通过ReSharper工具很方便地生成用例中定义的类和方法，如图：

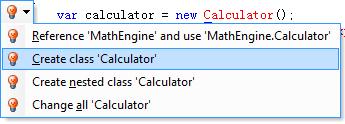
（三）面向对象的设计：既然是面向对象，首先我们从对象（表达式）入手，来看一个一般的四则混合运算表达式的解析过程：

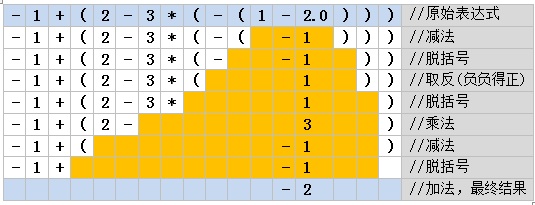
计算过程中我们总结出以下几点：

复杂的表达式都是由一些一元或二元的子表达式构成的
二元操作有两个操作数，如（加减乘除）
一元操作有一个操作数，如（脱括号，取反）
一个表达式的计算结果可以作为另一个表达式的操作数
乘除法优先于加减法求值
括号可以改变求值优先级
负数也可以当做对其绝对值的取反（如--1=1就相当于进行了两次取反操作）

所以，操作数和运算符构成了表达式，表达式结果又可以作为操作数。所以操作数和表达式具有相同的性质，我们把它抽象出来叫做节点（Node），节点之间的关系可以如下图表示：

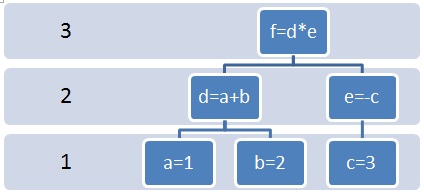
很明显，节点（Node）具有以下属性和行为：

节点属性
求值操作

其中不同的节点有不同的属性，一元节点有一个操作数，二元有两个操作数，而且二元操作又有着共同的行为；但是所有的节点都有公共的行为（求值），因此可以定义成【接口—抽象类—具体类】的方式，如图：

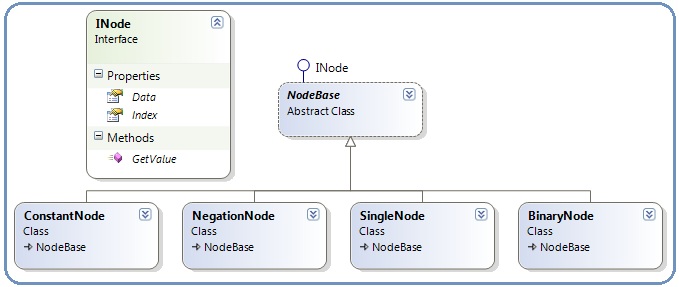
其中接口中定义的属性Data和Index用于解析过程中节点的信息，用于将来的表达式重构，这里可以忽略。上图中有四个具体类，“ConstantNode”和“NegationNode”分别是常量节点和取反节点，不需要多说；“SingleNode”是脱括号节点；BinaryNode是二元节点，为什么没有加减乘除呢？

其实可将BinaryNode定义为抽象类，再分别定义加减乘除四个具体类，之所为这样做是因为加减乘除除了运算逻辑外没有任何差别，这种把计算逻辑从其宿主中抽离出来的设计方式，通常也叫做策略模式，看下面的代码实现就可以一目了然：

public class BinaryNode : NodeBase
{
    private readonly INode _left;
    private readonly INode _right;
    private readonly Func<INode, INode, double> _function;
    public BinaryNode(INode left, INode right, int index, string data, Func<INode, INode, double> function)
    : base(index, data)
    {
        _left = left;
        _right = right;
        _function = function;
    }
    public override double GetValue()
    {
        return _function(_left, _right);
    }
}

好了，节点类的实现到此结束，下面就开始我们的核心类的设计——节点解析类！

我们在计算表达式的过程中，遵守了几个规则，即：

1．括号中的子表达式优先

2．内层括号优先于外层括号

3．乘除法优先于加减法

4． ‘-‘是取反运算符还是减法运算符取决于其前面是操作符还是操作数。

很明显，一个合法的表达式解析完成后应该剩下一个根节点，解析过程已经把各个子运算（节点）都保存在一个二叉树形式的结构中，求值也变成一个树形递归过程，即子节点先于父节点求值，遵守了优先级规则，所以我们的节点解析类只要按照优先级顺序从表达式中解析完了所有的节点就大功告成了。

面向对象的思路就是将类设计成各司其职的小类，避免功能庞大，结合以上分析需要考虑解析的优先级，我们可以将节点解析类（称为Finder），各个节点的Finder类各司其职，如图：

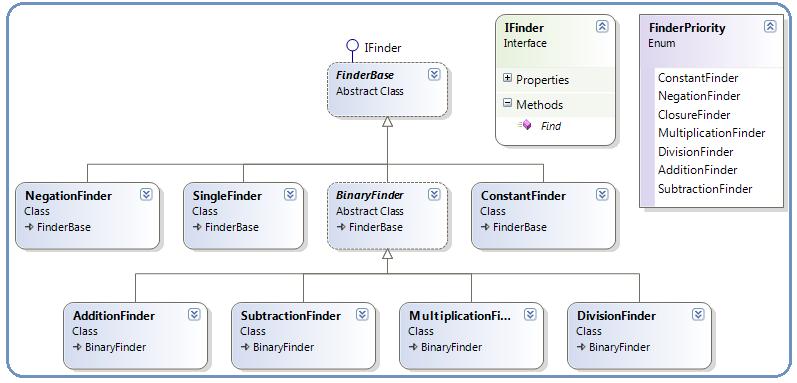
来看一下代码实现：

首先是接口IFinder，然后是抽象类FinderBase，它提供了一个Find方法，Find采用正则表达式匹配的方式来解析节点，具体的正则表达式和节点类型在具体类中实现：

    
public interface IFinder
{
    int Priority { get; }//不同的子式解析的优先级不一样，例如乘法要先于加法
    Calculator Calculator { set; }
    INode Find(string expression);
}
public abstract class FinderBase : IFinder
{
    public Calculator Calculator { get; set; }
    protected abstract string Rule { get; }
    public abstract int Priority { get; }
    private Regex _regex;
    private Regex Regex{get { return _regex ?? (_regex = new Regex(Rule)); }}
    protected abstract INode GenerateNode(string sourceExpression, string node, int index);
    protected Match Match { get; private set; }
    public INode Find(string expression)
    {
        Match = Regex.Match(expression);
        INode node = null;
        if (Match.Success)
        {
            node = GenerateNode(expression, Match.Value, Match.Index);
        }
        return node;
    }
    public static List<IFinder> GetAllFinders()
    {
        return Reflector.CreateInstances<FinderBase>().OfType<IFinder>().OrderBy(f => f.Priority).ToList();
    }
}

    
///<summary>
/// 常量，包括小数和整数(不包括负数，负数由NegationFinder（取反）运算处理)
///</summary>
public class ConstantFinder : FinderBase
{
    public override int Priority { get { return (int)FinderPriority.ConstantFinder; } }
    protected override string Rule
    {
        //(\-*\d+\.*\d+)匹配不到仅有1个数字的数如1,所以要与(\-*\d+)并用
        get { return @"(\d+\.*\d+)|(\d+)"; }
    }
    protected override INode GenerateNode(string sourceExpression, string data, int index)
    {
        return new ConstantNode(data, index, data);
    }
}

取反节点解析器，这个稍微有一点点复杂，主要是因为要与减法操作区别开来：

/// <summary>
/// 取反(负数)，如-a转成b
/// </summary>
public class NegationFinder : FinderBase
{
    public override int Priority { get { return (int)FinderPriority.NegationFinder; } }
    protected override string Rule
    {
        //注意：此处"-"匹配到的可能不是数值符号，也可能是减法运算符,在GenerateNode中处理
        get { return @"\-[a-j]+"; }
    }
    protected override INode GenerateNode(string sourceExpression, string data, int index)
    {
        if (Match.Index > 0)
        {
            var preChar = sourceExpression[index - 1];
            //如果前面一个字节是一个操作数，则“-”是一个减法操作符，不处理节点.
            if (preChar == ')' || (preChar >= 'a' && preChar <= 'j'))
            return null;
        }
        INode rightNode = Calculator.GetNode(data.Substring(1));
        return  new NegationNode(rightNode, index, data);
    }
}

再来看一下二元节点的Finder类，看看策略模式是如何工作的：

/// <summary>
/// 二元运算符:加减乘除等
/// </summary>
public abstract class BinaryFinder : FinderBase
{
    protected abstract char Symbal { get; }
    protected abstract Func<INode, INode, double> Function { get; }
    public override int Priority { get { return (int)FinderPriority.MultiplicationFinder; } }
    protected override string Rule
    {
        get { return @"[a-j]+@Symbal@[a-j]+".Replace("@Symbal@", "\\" + Symbal); }
    }
    protected override INode GenerateNode(string sourceExpression, string data, int index)
    {
        string[] ids = data.Split(Symbal);
        INode left = Calculator.GetNode(ids[0]);
        INode right = Calculator.GetNode(ids[1]);
        return new BinaryNode(left, right, index, data, Function);
    }
}
public class MultiplicationFinder : BinaryFinder
{
    protected override char Symbal { get { return '*'; } }
    protected override Func<INode, INode, double> Function { get { return ((l, r) => l.GetValue() * r.GetValue()); }}
    public override int Priority { get { return (int)FinderPriority.MultiplicationFinder; } }
}

策略模式的好处就是可以使我们的代码极为简洁，而且易于扩展，试想一下，如果我们要增加一个二元运算（乘方），使得四则混合编程五则混合，则只需要增加一个类似于MultiplicationFinder的类即可，代码也不过五六行。

好了，节点和节点解析类都已经完成，剩下的工作就易如反掌地去实现Calculator类了，代码：

public class Calculator
{
    public List<string> Log;//记录表达式解析与重构的过程
    private Dictionary<string, INode> _foundNodes;
    public double CalculateExpression(List<IFinder> finders, string expression)
    {
        CheckInputExpression(expression);
        expression = AdjustInputExpression(expression);
        finders.ForEach(f => f.Calculator = this);
        if (_foundNodes == null)
        _foundNodes = new Dictionary<string, INode>();
        else _foundNodes.Clear();
        Log = new List<string>();
        bool findOver = false;
            
        while (!findOver)
        {
            findOver = true;
            if (IsNode(expression))
            break;
            foreach (var finder in finders)
            {
                INode node = finder.Find(expression);
                if (node != null)
                {
                    var id = AddNode(node);
                    expression = RestructureExpression(expression, node, id);
                    Log.Add(expression);
                    findOver = false;
                    break; //表达式已被重构，需要从头重新解析
                }
            }
        }
        if (!IsNode(expression))
        throw new Exception("表达式不正确");
        if (_foundNodes.Count >= 1)
        return _foundNodes.Last().Value.GetValue();
        return double.NaN;
    }
}

值得注意的是，表达式在解析和重构过程中会出现新的节点类型，因此需要重新按照优先级解析重构后的表达式。直到只剩下一个节点（解析成功），或者找不到任何节点了（表达式错误）。当然，解析方法过程中还有很多可以改善的地方，例如性能提升等等！

与测试用例中调用不一样，我们在CalculateExpression中增加了一个参数List<IFinder> finders，（这时测试用例需要修改一下），

这个finers是各个节点解析类的实例，它们是怎么创建的呢？Reflector和Linq上场了：

public static IEnumerable<T> CreateInstances<T>()
{
    Type basic = typeof (T);
    var types = basic.Assembly.GetTypes();
    var result = (from t in types
    where basic.IsAssignableFrom(t) && !t.IsAbstract
    select (T) Activator.CreateInstance(t)).ToList();
    return result;
}
public static List<IFinder> GetAllFinders()
{
    return Reflector.CreateInstances<FinderBase>().OfType<IFinder>().OrderBy(f => f.Priority).ToList();
}

GetAllFinders()实例了从抽象类FinderBase继承的所有实体类，并通过Linq进行了优先级排序。仅仅一行代码，这就是Linq的强大功能。

好了，编译调试运行，该部分功能顺利结束，运行结果如图：

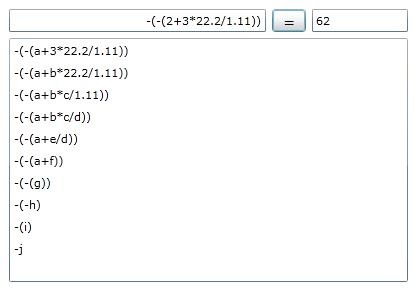
下一部分我们将添加常用的数学函数进入表达式，如Sin(),Avg()等等，使得功能更加丰富。

数学编程

第二部分：编程技能的简单应用

带括号的四则混合运算计算器（一）